Lecture 13

• Lecture 13
  • Video
  • Heuristic Functions
  • Uninformed vs Informed Search
  • Does heuristic search always give optimal solution
  • Admissible Heuristic
    • Examples
  • Dominance
  • Relaxed Problem
  • Constructing a Heuristic Function

Video

link

Heuristic Functions

• a technique for solving a prob more quickly when classic methoda re too slow, or for finding an approximate solution when classical methods fail to find any exact solutions
• achived by trading optimality, completenes, accuracy or precision for speed
• can be considered a shortcut
• heuristic function ranks alternatives in search algos at each branching step based on avaialble info to decide which branhc to follow
• it may approximate exact soln
• is a function used in informed search and it finds most promising path
• it takes current state of agent as its input and produces the estimation of how close agent is from the goal
• guaranteed to find a good soln in reasonable time, might not give best one
• estimates how close a state is to the goal
• represented by h(n) and calculates the cost of an optimal path b/w pair of states
• value is always positive
• estimate of cost of shortest path from node n to goal node
  • H can be extended to path: j(<n0,…nk>) = h(nk)
• h(n) uses only readily obtainable info (that is easy to compute) about a node
• admissible : h(n) is an underestimate if there’s no path from n to a goal that has apth less than h(n)
• i.e. h(n) is a lower bound on the cost of getting from n to the nearest goal
• If nodes are points on a Euclidean plane/space and cost is diatance, we can use Straight line distance from n to the closest goal as the value of h(n)
  • makes sense if there are obstacles or for other reasons not all adjacent nodes share arc
• If nodes are cells in frid and cost is #steps, use Manhattan Distance (L1)
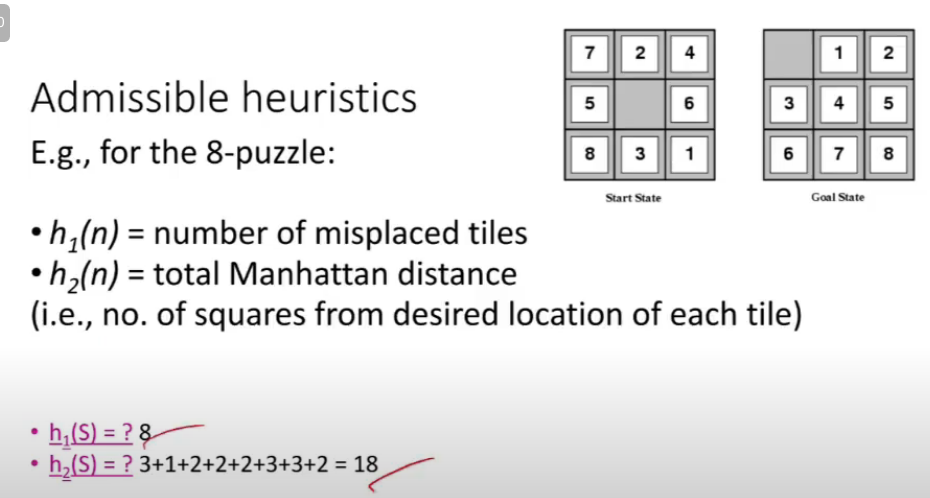
• in 8-puzzle, use number of moves b/w each tile’s current position and its position in solution

Uninformed vs Informed Search

• uninf expand nodes based on distance from start node
• inf use some estimate of distance to goal h(n), called heuristic
  • SLD b/w 2 points in a navigation problem(romnia wala)
  • #misplaced tiles in 9-puzzle
• heuristic is often result of thinking about a relaxed version of prob (romania me hamne sochlia ki stright road hai agar har 2 city ke beech me, then I won’t pick the other 2 sides of triangle)

Does heuristic search always give optimal solution

• depends upon heuristic

Admissible Heuristic

• G = set of goal nodes

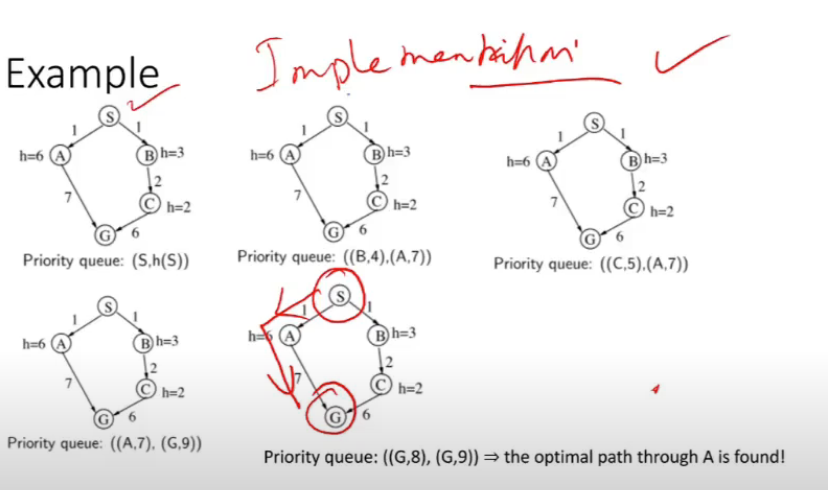
Examples

Dominance

Relaxed Problem

• prob with fewer restrictions on actions
• cost of an optimal soln to relaxed is admissible heuristic for original prob
• if rules of 8-puzzle are relaxed so that tile can move anywhere, h1(n) gives shortest soln
• if rules are relaxed so that a tile can move to any adjacen square, then h2(n) gives shortest soln

Constructing a Heuristic Function

• a cost minimizing serarch prob is a constrained optimizn prob
  • eg find a pth from A to B which minimizes distance traveled subject to constraint that robot cannot move through walls
• a relaxed version of prob is version of prob where one or more constraints have been dropped
  • eg: find path from a to b which minimizes dist traveled allowing agent to move through walls
  • a relaxed version will always return a value which is weakly smaller than origin : thus an admissible heuristic