Lecture 2

• Lecture 2
  • Video
  • Summary done so far
  • High Dimensional Data
  • Gamma Function
  • Nearest Neighbor Search
  • Problems with high dimensional Data

Video

link

Summary done so far

• Dimensionality concept

High Dimensional Data

• n dimensional vectors - last class me dekha
• Any point in n-d space is a n-d vector
• Similarity between points
  • Use distance between two points as the criteria
  • Dot product between two product gives cosine similarity
    • Similar vectors will give high dot product

Gamma Function

• generalization of factorial for real and complex numbers

Nearest Neighbor Search

• given some points in d-dim space
• and given a query point, find nearest neighbor
• 2d me I can visually determine as well
• In high-dimensional space, nearest neighbor loses meaning

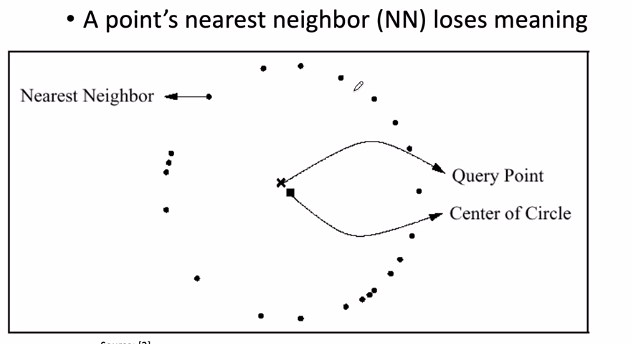
• The reason is the Concentration of Lp Norm
  • Manhattan and Eucledian dists are spl cases of Lp Norm
  • p = 1 => Manhattan, p = 2 => Euclidean

Problems with high dimensional Data

• collectively these probs are called Curse of Dimensionality (CoD)
  • Running time
  • Overfitting
  • Number of Samples reqd

• the given feature is not discriminated
  • i;.e. I cannot draw a vertical line and say one side is squares, and one is circles
  • so I am not able to distinguish 2 types of points in 1d space
  • so, let’s add one more dimension and maintain same density
    • 9 points in 1d => 9x9 points in 2d?
    • but we have 9 points only bhai
  • 
• 
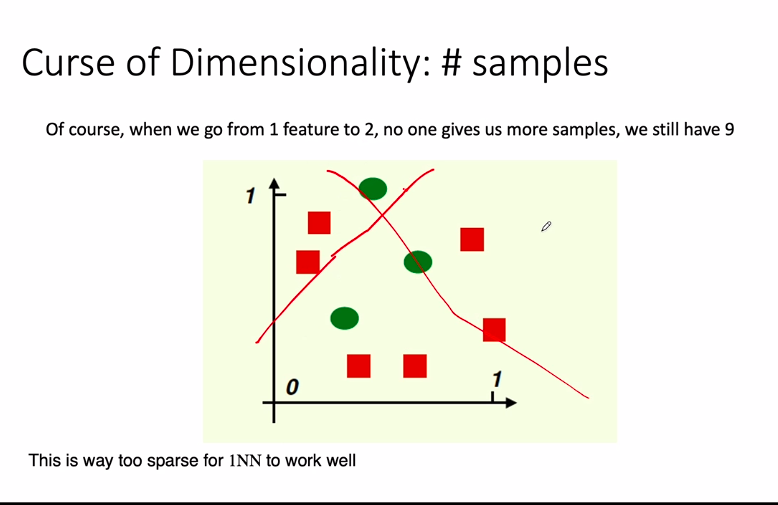
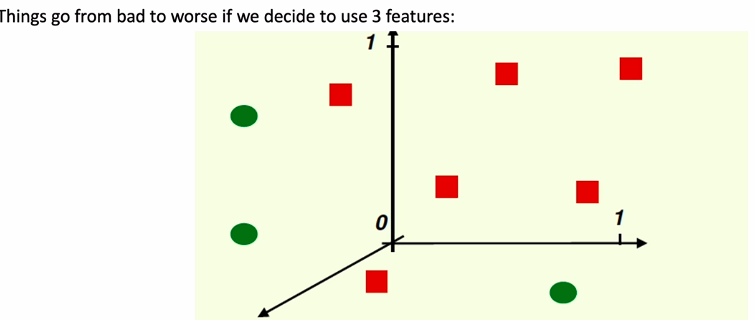
• Linearly Separable data
• what we can do to make data not linearly separable in lower dim space to make it linearly separable in high dim space
• to keep same density ,I will need 9x9x9 = 729 points but I only have 9 points
• so data become sparse
• 
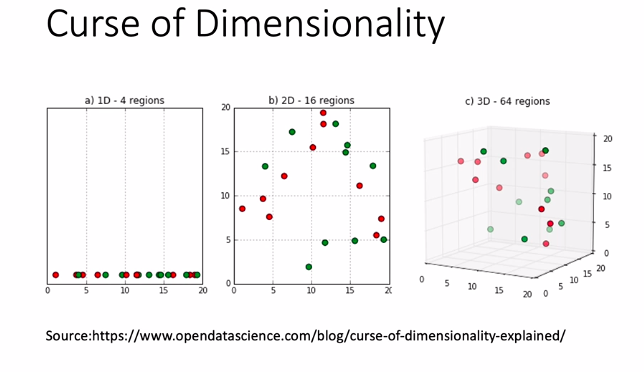
• and most of the techniques like 1nn do not work when data is sparse, bcz in high-dim spaces, concept of dist becomes meaning less, all appear at equidistant