Lecture 4

• Lecture 4
  • Lecture plan
  • Books
  • Topics to be covered
  • Introduction
  • Various types of optimization problems
  • Traditional and nontraditional or metaheuristic techniques
  • Some applications of optimization
  • A bit of history
  • Analytical method - unconstrained case
  • Analytical method - constrained case

Lecturer - Bijoy Krishna Mukherjee

Lecture plan

• module 1
  • nontraditional optimization
  • 6 lecs
• module 2
  • fuzzy logic
  • 9 lecs

Books

• red = module 1

Topics to be covered

• intro to traditional optimization - 2 lecs
• nontraditional optimization - Genetical aversion - 3L
• nontraditional optimization - PSO - 1L

Introduction

• method to find the best solution out of several feasible solutions
• first step is to express the criteria to judge the goodness of a solution as a function of factors wich influence the chosen criteria
  • this is known as objective function
• Mathematically

• bounds => we are confining search space

Various types of optimization problems

• unconstrained and constrained
• single and multiobjective
  • single objective function vs multiple
• static and dynamic
  • dynamic => differential equations are involved
  • static => all are algebraic equations
• linear programming and non-linear programming
• integer programming and real valued programming
• we will consider bold ones in course

Traditional and nontraditional or metaheuristic techniques

• traditional
  • based on pure mathematics
  • yields precise solutions
  • may not be suitable to solve complex real-world problems
• they both complement each other
• nontraditional try to solve acceptable soln quickly, maybe not accurate
• maximization problems can be converted to minimization problems by modifying obj functions as

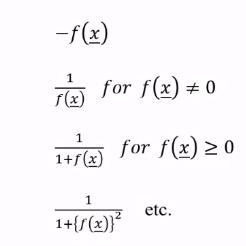
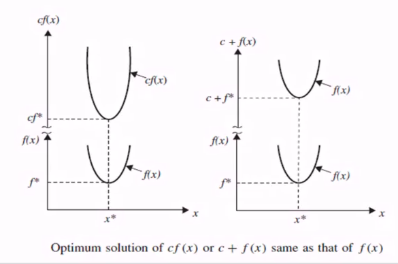
• following operations on the objective function will noe change optimum soln x*
  • multiplication/division of f(x) by a +ve const c
  • addition/subtr a const c from f(x)

Some applications of optimization

• almost all fields where numerical info is processed(science, engg, math, eco, commerce)
• relevant where technical or managerial decision making is involved or a trade-off is involved
• engg design applns usually have constraints since the variables cannot take arbitrary values and usually we want to minimize/maximize something
• eg designing a bridge, engg want to minimize cost while maintaining a certain min strength for the structure
• Control and signal processing applications (e.g. Kalman filter)
• many other probs can be cast as optimization problems
  • eg root finding, soln of overdetermined/underdetermined linear system of equations
    • Root Finding
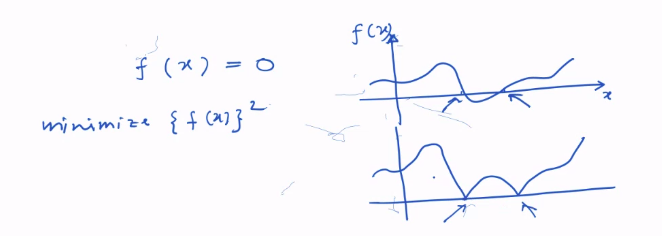
      • squaring f(x) made roots as min valued points
    • soln of overdetermined/underdetermined linear system of equations
      • overdetermined - we have more equations and less number of unknowns
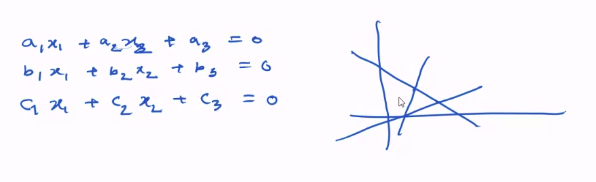
        • 3 eqns, 2 unknowns
        • from graph, no soln
        • so koi aisa point lia jo 2 ke intersection pe hai, so 3rd wala error dega, square and get sum total error
        • find a point which has least error - LEAST Square Error solution
        • write it as AX = B

        • and minimize 2 norm

          AX-B

        • soln can be found by pseudo inverse
          • X = (A’A)inv AB, A’ = A transpose
      • underdetermined
        • less equations and more unknowns
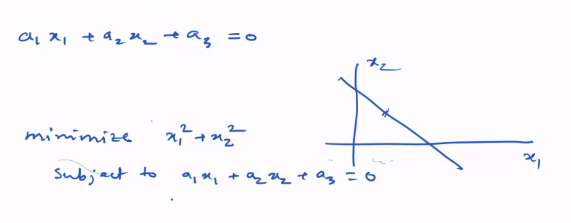
        • solution again by pseudoinverse
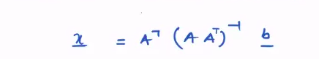
        • this is least energy solution
        • we need to find a point on line which is closest to origin

A bit of history

Analytical method - unconstrained case

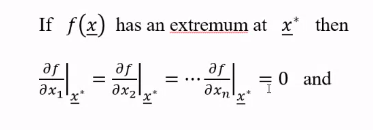
• all partial derivatives at extremum are zero
• whether it’s max or min, will be given by second order - matrix is
• it is multivariate extension of what we did in +2
• Positive definite matrix
  • determinants of leading principal minors are all positive
  • 
• Negative definite matrix
  • 

Analytical method - constrained case

• lagrange multiplier method

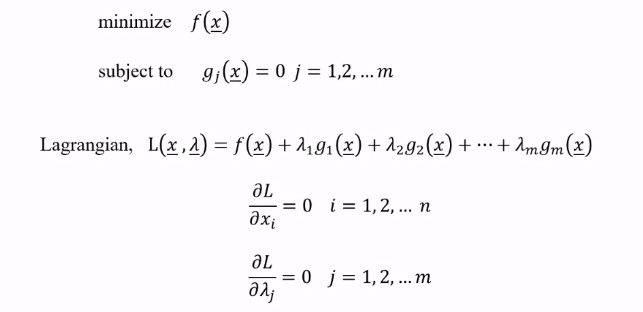
• converted equality constrained problem to unconstrained problem